The resistance and temperature characteristics of a thermistor can be approximated by equation 1.

\[ 　 \begin{pmatrix} eq1 \end{pmatrix} \qquad R = R_o \ exp \begin{Bmatrix} B \begin{pmatrix} 1 / T-1 / To \end{pmatrix} \end{Bmatrix} \]

R : resistance at absolute temperature T(K)
R₀ : resistance at absolute temperature T₀(K)
B : B value
※T(K)= t(˚C)+273.15

The B value for the thermistor characteristics is not fixed, but can vary by as much as 5K/ ̊C according to the material composition. Therefore equation 1 may yield different results from actual values if applied over a wide temperature range.

By taking the B value in equation 1 as a function of temperature, as shown in equation 2, the difference with the actual value can be minimized.

\[ 　 \begin{pmatrix} eq 2 \end{pmatrix} \qquad B_t = CT^2 + DT + E \]

C, D, and E are constants.
The B value distribution caused by manufacturing conditions will change the constant E, but will have no effect on constants C or D. This means, when taking into account the distribution of B value, it is enough to do it with the constant E only.

• Calculation for constants C, D and E

Using equations 3~6, constants C, D and E can be determined through four temperature and resistance value data points\( \begin{pmatrix} T_0,R_0 \end{pmatrix}.\begin{pmatrix} T_1,R_1 \end{pmatrix}.\begin{pmatrix} T_2,R_2 \end{pmatrix}and\begin{pmatrix} T_3,R_3 \end{pmatrix} \).
With equation 3, \( B_1,B_2 \) and \( B_3 \), can be determined from the resistancevalues for \( T_0 \) and \( T_1,T_2,T_3 \) and then substituted into the equations below.

\[ \begin{eqnarray} 　\begin{pmatrix} eq 3 \end{pmatrix} \qquad B_n &=& \frac{ln \begin{pmatrix} R_n/R_o \end{pmatrix}}{ \frac{1}{T_n} - \frac{1}{T_0} } \\[8px] 　\begin{pmatrix} eq 4 \end{pmatrix} \qquad C &=& \frac{ \begin{pmatrix} B_1 - B_2 \end{pmatrix} \begin{pmatrix} T_2 - T_3 \end{pmatrix} - \begin{pmatrix} B_2 - B_3 \end{pmatrix} \begin{pmatrix} T_1 - T_2 \end{pmatrix} }{ \begin{pmatrix} T_1 - T_2 \end{pmatrix} \begin{pmatrix} T_2 - T_3 \end{pmatrix} \begin{pmatrix} T_1 - T_3 \end{pmatrix} } \\[8px] 　\begin{pmatrix} eq 5 \end{pmatrix} \qquad D &=& \frac{ B_1-B_2-C\begin{pmatrix} T_1 + T_2 \end{pmatrix}\begin{pmatrix} T_1 - T_2 \end{pmatrix} }{ \begin{pmatrix} T_1 - T_2 \end{pmatrix} } \\[8px] 　\begin{pmatrix} eq 6 \end{pmatrix} \qquad E &=& B_1-DT_1-CT_1 \cdot T_1 \end{eqnarray} \]

• Example

Using a resistance-temperature characteristic chart, the resistance value over the range of 10 ̊C~30 ̊C is sought for a thermistor with a resistance of 5kΩ and a B value deflection of 50K at 25 ̊C.

• Process

1. Determine the constants C, D and E from the resistance-temperature chart.

\[ T_0=25+273.15 \qquad T_1=10+273.15 \qquad T_2=20+273.15 \qquad T_3=30+273.15 \]

2. \( B_T=CT^2+DT+E+50 \) ; substitute the value into equation and solve for \( B_T \)
3. \( R=5 exp \begin{Bmatrix} B_T \begin{pmatrix} 1/T-1/298.15 \end{pmatrix}\end{Bmatrix} \) ; substitute the values into equation and solve for R

※T：10＋273.15～30＋273.15

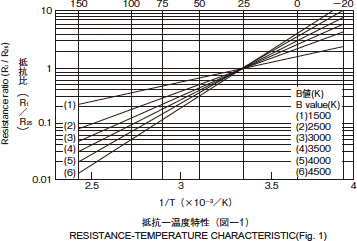
• Results of plotting the resistance-temperature characteristics are shown figure 1