News
-
We have renewed the electronic materials business website
APPLICATION
SEARCH by application/use
PRODUCTS
Products Lineup

Products
We introduce unique, high-value products that make use of the materials produced by our group.
- Precision Silicon Products
- Gold-tin (AuSn) Alloy Solder Paste
- Sol-Gel Solutions
- Low Alpha Solders
- NTC Thermistors
- Thermistor Sensors
- Surge Absorbers
- Columnar Crystal Silicon
- Perfluoroalkylsulfonyl Compounds
- Transparent Conductive Materials
- White Electro-conductive Materials
- Insulation Black Pigment
- Solar Heat-ray Shielding
- Seal Products
PICK UP

DA53 Series
The DA53 Series has a micro-gap cut to an accuracy of several tens of microns for rapid response against induced lightning and electrostatic discharges.Ideal for protecting power supplies from power-line surge voltage.
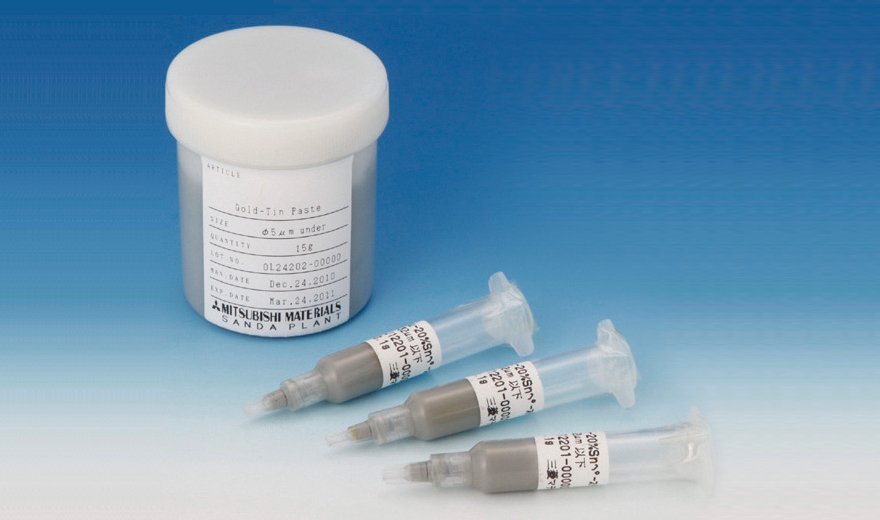
Gold-tin (AuSn) Alloy Solder Paste
Mitsubishi Materials' Gold-tin(AuSn) alloy paste offers high process flexibility.

New KH05 Series
The KH Series are wire-bondable flake style NTC Thermistors
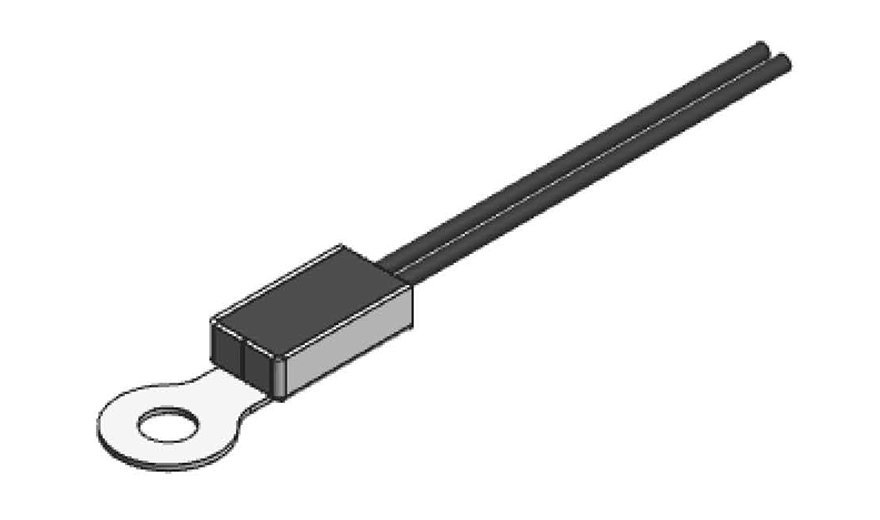
New STS-74
The STS-74 is a ring-tongue NTC Thermistor for measuring surface temperatures.
SOLUTION
SOLUTIONS / KNOWLEDGE

Solution
We have useful information like usage examples, technical information, and explanations for using our products.
- Thermal Management Solution for Mobility
- Characteristics of Gold-Tin Alloy Paste
- Characteristics of Low Alpha Plating Chemicals
- Basic Characteristics of NTC Thermistors
- Example of Using NTC Thermistors
- Chip Thermistor Resistance Simulator
- Basic Characteristics of Surge Absorbers
- Surge Absorber Examples
- Surge Countermeasures


